a. Pengertian
Analisis Kovarian atau ANCOVA merupakan teknik analisis yang berguna
untuk meningkatkan presisi sebuah percobaan karena didalamnya dilakukan
pengaturan terhadap pengaruh peubah bebas lain yang tidak terkontrol. Peubah
bebas lain yang tidak terkontrol disebut sebagai variabel kovariat. ANCOVA
digunakan jika peubah bebas mencakup skala numerik dan kategorik. ANCOVA
merupakan penggabungan antara uji komparatif dan korelasional.
Pada
ANCOVA dilakukan uji perbandingan sekaligus hubungan (korelasi). Analisis
dilakukan dengan pembandingan variabel dependen (Y) ditinjau dari variabel
bebas (X1) sekaligus menghubungkan variabel dependen tersebut dengan variabel
bebas lainnya (X2). Variabel bebas yang digunakan untuk memprediksi dinamakan
dengan variabel kovariat.
Dalam ANCOVA, digunakan konsep ANOVA
dan analisis regresi dimana:
Anova digunakan untuk menguji
perbandingan variabel tergantung (Y) ditinjau dari variabel bebas (X1)
Regresi
digunakan untuk memprediksi variabel tergantung (Y) melalui variabel bebas (X2)
Karakteristik
variabel pengujian ANCOVA adalah sebagai berikut :
Variabel dependen (Y):
Numerik/kontinu (Interval atau rasio)
Variabel bebas (X1): Kategorik
(nominal atau ordinal)
Variabel kovariat (X2):
Numerik/kontinu (interval atau rasio)
b. Tujuan
Tujuan
ANCOVA adalah untuk mengetahui/melihat pengaruh perlakuan terhadap peubah
respon dengan mengontrol peubah lain yang kuantitatif.
c.
Model
Persamaan
Model ANCOVA dengan satu covariate:
yij = µ + τi + βxij
+ εij
, i = 1,2,….,a j = 1,2,….,ni
dimana:
yij : nilai peubah respon pada perlakuan ke-i
observasi ke-j
xij : nilai covariate pada observasi yang
bersesuaian dengan yij
τi : pengaruh perlakuan ke-i
β : koefisien regresi linier
εij : random error
a : banyaknya kategori pada perlakuan
ni : banyaknya observasi pada kategori ke-i
d.
Asumsi
yang harus terpenuhi
Asumsi dalam ANCOVA
1. X adalah fixed,
diukur tanpa error dan independen terhadap perlakuan (tidak dipengaruhi oleh
perlakuan).
2. εij mengikuti sebaran NID (o,σ2).
3. β ≠ 0 yang mengindikasikan bahwa antara x dan y
terdapat hubungan linier.
4. Ada hubungan linier antara variabel kovariat dengan
variabel dependen.
e.
Pengujian
Hipotesis
1.
Pengujian untuk mengetahui pengaruh perbedaaan
perlakuan terhadap peubah respon, dengan menghilangkan pengaruh covariate.
Hipotesis
H0 : τ1 = τ2 = ...= τa
= 0 (Tidak ada pengaruh perbedaaan perlakuan terhadap peubah respon)
H1 :
sekurang-kurangnya ada satu τi ≠ 0, i = 1, 2, ...a (Ada pengaruh
perbedaaan perlakuan terhadap peubah respon)
Kriteria Keputusan :
Jika angka
Sig.>0.05 maka H0 tidak ditolak, yang berarti tidak ada pengaruh
perbedaan perlakuan terhadap peubah respon.
Jika angka
Sig.<0.05 maka H0 ditolak, yang berarti ada pengaruh perbedaan
perlakuan terhadap peubah respon.
2.
Pengujian untuk mengetahui hubungan linier
antara kovariat dengan peubah respon dengan menghilangkan pengaruh perlakuan.
Hipotesis
H0 : β = 0 (Tidak ada hubungan linier antara
kovariat dengan peubah respon)
H1 : β ≠ 0 (Ada hubungan linier antara
kovariat dengan peubah respon)
Kriteria keputusan
Jika angka Sig. >
0.05 maka H0 tidak ditolak, yang berarti tidak ada hubungan linier antara
kovariat dengan peubah respon
Jika angka sig. <
0.05 maka H0 ditolak, yang berarti ada hubungan linier antara kovariat dengan
peubah respon

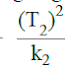



0 Komentar untuk : Analysis of Covariance