Uji lanjut Scott-Knott merupakan metode
perbandingan nilai tengah perlakuan yang mengurutkan dan mengelompokkan nilai
tengah kedalam kelompok-kelompok yang
tidak saling tumpang
tindih. Uji lanjut ini dapat digunakan untuk
data dengan jumlah perlakuan besar (Jelihovschi dan
Faria 2013).
Menurut Scott dan Knott (1974), uji lanjut Scott-Knott atau Scott-Knott test mengelompokkan gugus nilai tengah perlakuan saling bebas, yang diurutkan dengan asumsi nilai tengah menyebar normal dan penduga ragam atau variance adalah menyebar Chi-Square.
Hipotesis dari uji lanjut Scott-Knott adalah:
H0 : µi = µ
, i =1,2,3,...,k (nilai tengah k perlakuan adalah sama)
H1 : µi sama dengan salah satu dari m1 atau m2, (m1 dan m2 mewakili nilai tengah dua gugus yang belum diketahui)
Tahapan perhitungan uji Lanjut Scott-Knott:
1. Menghitung jumlah kuadrat antar pasangan gugus (B0) dari k nilai tengah perlakuan yang akan dikelompokkan.
Banyaknya B0 yang terbentuk ada sebanyak k-1.
Rumus jumlah kuadrat antar pasangan gugus (B0) adalah sebagai berikut:
T1 = jumlah nilai tengah kelompok 1 (awalnya, kelompok 1 terdiri dari satu nilai tengah tertinggi atau terendah pertama dari hasil mengurutkan)
T2 = jumlah nilai tengah kelompok 2
k1 = banyaknya perlakuan pada kelompok 1
k2 = banyaknya perlakuan pada kelompok 2
Lakukan hal ini hingga kelompok 1 terdiri dari seluruh k perlakuan dikurangi 1 perlakuan urutan terakhir sebagai anggota kelompok 2.
2. Memilih nilai jumlah kuadrat antar pasangan gugus yang maksimum atau B0 maksimum
3. Menghitung statistik uji
statistik uji λ menyebar chi-square dengan derajat bebas V0, dan π = 3,14. Ragam perlakuan adalah penduga kemungkinan maksimum dari σ2/r dengan r adalah banyaknya ulangan (kelompok).
4. Uji hipotesis
jika λ > χ2 (α, db=k/ π-2)
maka tolak H0, yaitu kedua gugus nilai tengah yang diuji dianggap tidak homogen. Prosedur perhitungan masing-masing gugus diulang sampai mendapatkan hasil terima H0 atau hanya terdapat satu perlakuan pada satu gugus.

 Iterasi
1
Iterasi
1
Tahapan kedua: Menghitung jumlah kuadrat antar pasangan gugus B0(i) dengan i =1, 2,..,5
Tahapan ketiga: menentukan nilai B0 maksimum
B0 maks = B0 (2) = 127,27

jika λ > χ2 (α, db=k/ π-2)
maka tolak H0, yaitu kedua gugus nilai tengah yang diuji dianggap tidak homogen. Prosedur perhitungan masing-masing gugus diulang sampai mendapatkan hasil terima H0 atau hanya terdapat satu perlakuan pada satu gugus.
Ilustrasi perhitungan:
Suatu percobaan
dengan menggunakan
Rancangan Acak Lengkap dengan limaulangan dan enam erlakuan. Setelah dilakukan analisis ragam disimpulkan
bahwa terdapat
perbedaan yang
nyata antar perlakuan terhadap respon.
Nilai tengah delapan perlakuan yang sudah diurutkan adalah 28.82, 23.98, 19.92, 18.70, 14.64,
13.26
Jawab:
Tabel Analisis ragam
Sumber Ragam
|
DB
|
JK
|
KT
|
F P
|
Perlakuan
|
5
|
847.047
|
169.409
|
14.37
0.000
|
Galat
|
24
|
282.298
|
11.789
|
|
Total
|
29
|
1192.975
|
Tahapan pertama: Mengurutkan nilai tengah perlakuan (secara menurun) k = 6, v0=db=24
B0 maks = B0 (2) = 127,27
Keputusan: λ = 23,247 > χ2 (α=0,05, db=k/ π-2=5) = 11,07 --> tolak H0
Kesimpulan: Kedua gugus kelompok tidak homogen. Oleh karena itu, lakukan
tahapan 2-5 untuk setiap pasangan gugus.
Contoh hasil keluaran software R i386 3.0.2 package (ScottKnott_1.2-4):
Notes: warna yang berbeda menunjukkan kelompok yang berbeda.











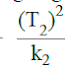
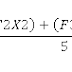


1 Komentar untuk : Scott-Knott Test
Aplikasi untuk scott knott apa gan